An overview of Visual Cryptography and implementations of the main state-of-the-art techniques in the VCrytpure open-source project.

cover

Cryptography is typically bypassed, not penetrated. ― Adi Shamir

Before proceeding

This post is an extract translated from my “Crittografia Visuale” article (written in Italian) available at https://blog.rev3rse.it/crittografia-visuale/ where Visual Cryptography is presented along with the open source project VCrypture - the complete code is available at https://github.com/UniCT-WebDevelopment/VCrypture.

Many people have long argued that the human brain will one day be able to replace a computer. While it may seem unreal, in a sense, this is partly possible (actually it has been for more than twenty years!). In 1994 Moni Naor and Adi Shamir introduced Visual Cryptography (VC), a particular cryptographic technique that allows to encode visual information (images) in such a way that the decoding process can be carried out by the human visual system, without the aid of any digital device at all.

In this article we present a brief overview of the main Visual Cryptography techniques, existing in the literature for different types of images (binary, greyscale, colour), and propose some implementations. These are gathered in VCrypture, a project developed by my dear friend and colleague G.T. and me.

VC vs Cryptography

The classic encryption operation consists of a plaintext and a key to be taken as input and, as output, it returns a cyphertext. Each of these three elements is designated for a very specific task, so if we were to exchange the roles of the key with the cyphertext and provide the decryption algorithm with the inverted pair as input - assuming the key and cryptotext have the same length and they can be interchanged from a syntactic point of view -, the result would certainly be something incomprehensible. In summary, the key must fulfil the role of key and, at the same time, the cryptotext must maintain the task of cryptotext. However, in the visual cryptographic schemes analysed below, we will see that the concept of key and cryptogram are completely interchangeable - note that as images we replace the suffix -text with the suffix -gram. In particular, given an input image (the equivalent of plaintext) for encryption, we will obtain two or more images of the same size (not necessarily the same as the input image’s), called shares. There is no way to distinguish the key share from cryptogram shares, as these are completely interchangeable. For such reason, it is more correct to refer to the terms share_A, share_B, etc., in general, as the semantics of either the key or cryptogram can be attributed to them in a subjective way.

The substantial difference, however, that distinguishes visual cryptography from the classic one lies in the fact that the decryption process does not require any computation. We will soon understand better how the human visual system can replace a computer to decode an image.

Visual Cryptography Techniques

In the next paragraphs, we will present a description of the visual cryptography schemes that we have included in the VCrypture project as well as describe their implementations in Python. For each of the schemes, there is a module with the same name as the authors, within the VCrypture-API component.

Binary VC

Naor-Shamir Example

Naor and Shamir wondered if it was possible to divide an image into n parts so that a person having all the n parts could be able to reconstruct the starting image, with the specific requirement that any set of n-1 parts would reveal no information. The authors published the Visual Cryptogrphy article in which they presented this very technique. The Naor-Shamir scheme is safe as long as a key is not reused more than once. In other words, the visual cryptography technique proposed by the authors is the “visual” equivalent of OTP (One-Time-Pad), a classic demonstrable cryptographic algorithm that is secure in the event that the encryption key is used only once - see also my article about TOTP. Note that OTP uses the XOR operator. In this paragraph, we present an implementation of the Naor-Shamir algorithm with a number of shares equal to 2. The algorithm is lossy, as the input image is converted into the binary mode in order to perform the subsequent operations correctly.

The encryption algorithm associates two 2x2 matrices to each pixel, which represent the two shares of the pixel. Each matrix must also have two black and two white pixels. Similarly, we can say that each of the pixels of the starting image will be divided into four sub-pixels, once for the first share and another time for the second share. This way, the two shares will be built pixel by pixel and, seen separately, they will have no meaning - each share will appear as if it were composed only of salt-and-pepper noise. The size of the shares will therefore be double the starting image. The rule to follow in order to assign the pixel values in the share images is very simple: if the pixel of the original image is black, the 2x2 matrices in the shares must be complementary. When these are overlapped, the black colour will appear as a result.

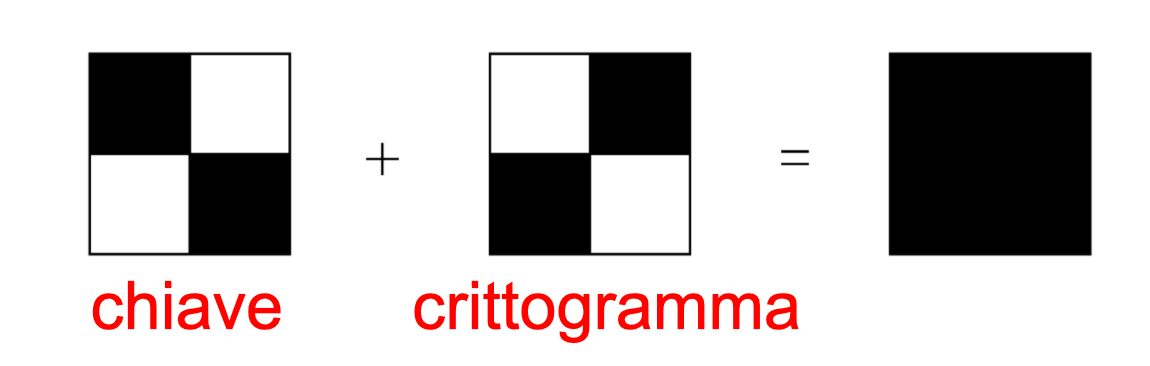black Side note for non-Italian people: chiave = key, crittogramma = cryptogram.

Conversely, if the pixel of the original image is white, the quadruples of pixels in the shares must match. In this case, however, when the two 2x2 matrices are overlapped, the result will be grey. It should be noted that the human eye will interpolate the result and interpret it as white.

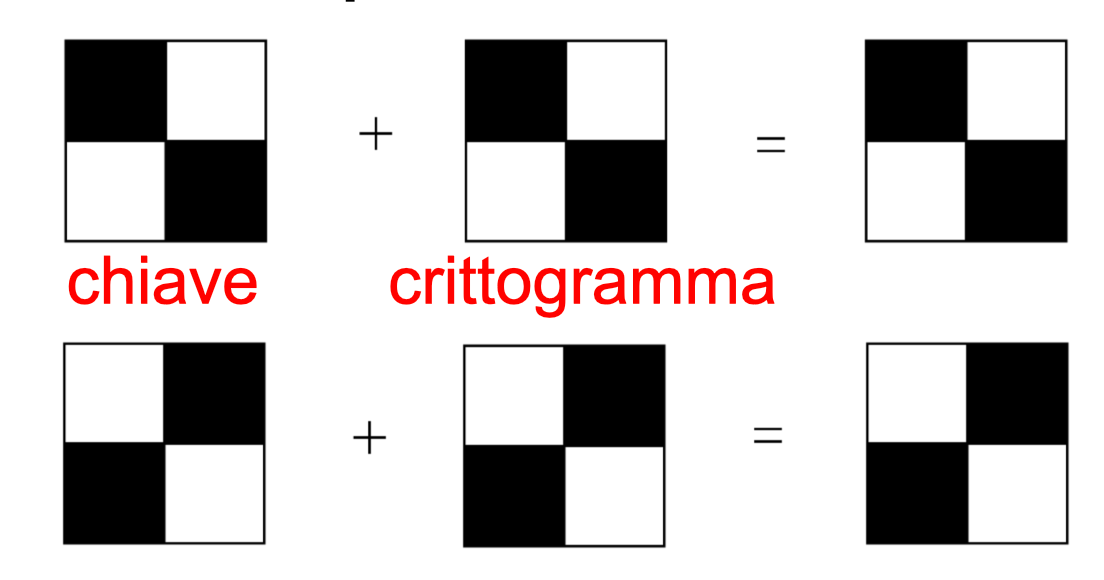white Side note for non-Italian people: chiave = key, crittogramma = cryptogram.

Below is the code snippet for the operations described above:

patterns = ((1, 1, 0, 0), (1, 0, 1, 0), (1, 0, 0, 1),
            (0, 1, 1, 0), (0, 1, 0, 1), (0, 0, 1, 1))

with Image.open(source) as secret:
  # Convert the input image to binary
  secret = secret.convert('1')

  # Prepare the two shares
  (width, height) = secret.size
  share_size = tuple(s * 2 for s in secret.size)
  share_A = Image.new('1', share_size)
  draw_A = ImageDraw.Draw(share_A)
  share_B = Image.new('1', share_size)
  draw_B = ImageDraw.Draw(share_B)

  # Cycle through pixels
  for x in range(width):
    for y in range(height):
      pixel = secret.getpixel((x, y))
      pat = random.choice(patterns)
      # Share A will always get the pattern
      draw_A.point((x * 2, y * 2), pat[0])
      draw_A.point((x * 2 + 1, y * 2), pat[1])
      draw_A.point((x * 2, y * 2 + 1), pat[2])
      draw_A.point((x * 2 + 1, y * 2 + 1), pat[3])
      if pixel == 0:  # B gets the anti-pattern
        draw_B.point((x * 2, y * 2), 1 - pat[0])
        draw_B.point((x * 2 + 1, y * 2), 1 - pat[1])
        draw_B.point((x * 2, y * 2 + 1), 1 - pat[2])
        draw_B.point((x * 2 + 1, y * 2 + 1), 1 - pat[3])
      else:
        draw_B.point((x * 2, y * 2), pat[0])
        draw_B.point((x * 2 + 1, y * 2), pat[1])
        draw_B.point((x * 2, y * 2 + 1), pat[2])
        draw_B.point((x * 2 + 1, y * 2 + 1), pat[3])

The decryption algorithm is very simple as it just simulates a manual overlap, namely the interpolation of the human eye, of the two shares:

# Overlap shares to get the secret
secret = Image.new('1', share_A.size)
secret_draw = ImageDraw.Draw(secret)

for x in range(secret.size[0]):
  for y in range(secret.size[1]):
    p1 = share_A.getpixel((x, y)) & 1
    p2 = share_B.getpixel((x, y)) & 1
    secret_draw.point((x, y), p1 & p2)

In addition to the 2x2 scheme, it is also possible to extend the original technique to four levels of grey, using 3x3 matrices, and so on. It is also possible to use a threshold scheme in which an image is encoded in N shares such that any overlapping K (K < N) shares allow the image to be obtained, while fewer than K do not. We will talk about the threshold scheme in the paragraph dedicated to colour images.

Greyscale VC

Taghaddos-Latif Example

Naor and Shamir’s original idea can be further extended in other ways, as illustrated in the Visual Cryptography for gray-scale Images Using Bit-level article by Taghaddos and Latif. Let’s jump from binary images to greyscale ones. Taghaddos-Latif uses the same size multiplier as Naor-Shamir and, also in this case, the result of the encryption algorithm is composed of two share images. This pattern is thus lossy, too.

The encryption algorithm uses the same patterns as the previous scheme. The extra complication here is due to the fact that now we no longer work with binary values, but greyscale with 8 bits (bitplane), so we have to add an additional cycle to scroll through the 8 bits of each pixel:

patterns = ((1, 1, 0, 0), (1, 0, 1, 0), (1, 0, 0, 1),
            (0, 1, 1, 0), (0, 1, 0, 1), (0, 0, 1, 1))

with Image.open(source) as secret:
  # Enforce greyscale mode
  if secret.mode != 'L':
    secret = secret.convert('L')

  # Cycle through pixels
  for x in range(0, width):
    for y in range(0, height):
      shareA_colours = [0, 0, 0, 0]
      shareB_colours = [0, 0, 0, 0]
        for b in range(8):
          pattern = random.choice(patterns)
          if secret.getpixel((x, y)) >> b & 1:
            for i in range(len(shareA_colours)):
              shareA_colours[i] |= (pattern[i] << b)
              shareB_colours[i] = shareA_colours[i]
          else:
            for i in range(len(shareA_colours)):
              shareA_colours[i] |= (pattern[i] << b)
              shareB_colours[i] |= ((1-pattern[i]) << b)
        _draw_block(draw_A, (x, y), shareA_colours)
        _draw_block(draw_B, (x, y), shareB_colours)

The decryption is nearly similar to the Naor-Shamir scheme:

# Overlap shares to get the secret
secret = Image.new('L', share_A.size)
secret_draw = ImageDraw.Draw(secret)

for x in range(secret.size[0]):
  for y in range(secret.size[1]):
    p1 = share_A.getpixel((x, y))
    p2 = share_B.getpixel((x, y))
    secret_draw.point((x, y), p1 & p2)

The results obtained with this scheme are, for 7 more bits reasons, better than the case proposed above.

RGB VC

Dhiman-Kasana EVCT(N, N) Example, share_A

Visual Cryptography is also applicable to colour images, but with some clarification. In this case, in fact, we will not speak of visual cryptography in the “pure” sense of the term, as we have the addition of a technique that is often confused with cryptography: steganography. This consists of hiding - beware that hiding does not mean encrypting in the cryptographic sense of the term! - information for communication between interlocutors. For colour images, in the Extended visual cryptography techniques for true color images article, Dhiman and Kasana propose two lossless methodologies (without loss of quality) that mix steganography with visual cryptography. It should be noted that in this regard we speak of Extended Visual Cryptography Techniques (EVCT). The schemes proposed by the authors can be classified as threshold schemes, defined as EVCT (N, N) and EVCT (K, N), with K < N. In particular, we have N = 3 and K = 2.

Remember that a colour image in the RGB space consists of three channels: Red, Green and Blue. In EVCT (3, 3) the first share contains the R component, the second share contains the G component and, finally, the last share contains the B component of the starting image. All of the three cryptograms - more generally all of the Ns - are necessary in order to reconstruct the hidden image. In the case of EVCT (2, 3), however, only two of the three shares are required to be able to reconstruct the secret. Essentially, the first share contains the RG components, the second the GB components and the third the RB components of the starting image. It is therefore easy to understand that in both schemes the shares are meaningful, as they contain the “cover” images and information on the secret image. The role of the covers is to avoid any suspicion that there is something hidden inside. In this regard as of our implementation, we make use of LoremPicsum, a free service from which we download random covers of the same size as the input image. Before proceeding, it should be clear that the Dhiman-Kasana schemes are quite expensive in terms of performance, as the size multiplier is 5 (each pixel is broken down into a 5x5 block). The components are, in particular, distributed as shown in the figure:

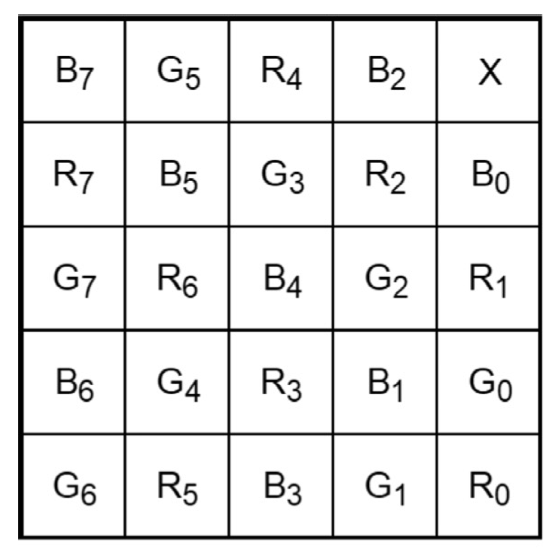
Dhiman-Kasana Components

The last pixel on the top right is left unchanged. For simplicity, we will only illustrate the algorithms of the EVCT (N, N) scheme, since in the case of the (K, N) scheme it is a matter of following the same reasoning, with the addition of including the information of two channels at a time (RG, GB, RB) in each share - however, remember that the complete code can be viewed on the VCrypture project repository.

The encryption algorithm builds a 5x5 block in each of the three shares for each pixel of the original image, following the pattern just described. It then proceeds by filling the 8 bits of each channel following the rule according to which if a bit is 1 it must be filled with black colour, otherwise dark grey:

components = {
  'R': ((4, 4),(4, 2),(3, 1),(2, 3),(2, 0),(1, 4),(1, 2),(0, 1)),
  'G': ((4, 3),(3, 4),(3, 2),(2, 1),(1, 3),(1, 0),(0, 4),(0, 2)),
  'B': ((4, 1),(3, 3),(3, 0),(2, 4),(2, 2),(1, 1),(0, 3),(0, 0))
}

def _enc_bit(secret_bit: bool) -> Tuple[int, int, int]:
  return (0, 0, 0) if secret_bit else (30, 30, 30)

x = 0
for i in range(width):
  y = 0
  for j in range(height):
    secret_pixel = secret.getpixel((i, j))
    for index, channel in enumerate(components.keys()):
      cover_pixel = covers[index].getpixel((i, j))
      with Image.new('RGB', (5, 5), cover_pixel) as block:
        block_draw = ImageDraw.Draw(block)
        for b, cell in enumerate(components[channel]):
          block_draw.point(cell,
                _enc_bit(secret_pixel[index] >> b & 1))
        shares[index].paste(block, (x, y, x + 5, y + 5))
    y += 5
  x += 5

The decryption algorithm uses the XOR operator to overlap the three shares and extract the information from the secret image contained in the 5x5 blocks of the three RGB components:

def _dec_bit(secret_pixel: Tuple[int, int, int]) -> bool:
  return secret_pixel == (0, 0, 0)

for cover in covers:
  ch = cover.info['CH']
  ch_index = 0 if ch == 'R' else 1 if ch == 'G' else 2
  x = 0
  for i in range(0, width, 5):
    y = 0
    for j in range(0, height, 5):
      sub = cover.crop((i, j, i + 5, j + 5))
      colour = 0
      for b, cell in enumerate(components[ch]):
        colour |= _dec_bit(sub.getpixel(cell)) << b
      s_colour = list(secret.getpixel((x, y)))
      s_colour[ch_index] = colour
      secret_draw.point((x, y), tuple(s_colour))
      y += 1
    x += 1

The schemes proposed by Dhiman and Kasana are the best among those illustrated in this article, as they present lossless algorithms from which it is possible to reconstruct the starting image entirely as it was. However, this comes at a price in terms of time performance and makes use of steganography, which influences the algorithms to be deterministic.

Conclusions

Visual Cryptography is an interesting and very powerful technique. Thanks to the variety of schemes it is possible to exploit several characteristics for multiple types of images, from binary images for which we have illustrated the Naor-Shamir algorithm, to greyscale images with the Taghaddos-Latif algorithm, to conclude with images in colour with the two extended visual cryptography schemes introduced by Dhiman-Kasana. Visual Cryptography applications can be different. Among these, we can mention: customer-bank authentication, verifiable receipts in e-voting, and sharing of medical images. In the first case, the bank sends the customer the key share on vinyl and publishes the cryptogram share on the network, so the user decrypts and reads the password. In the case of e-voting, the voter receives a share of the receipt. As for medical images, the use of visual cryptography schemes certainly ensures the confidentiality of sensitive information to be preserved. In each of these cases, the human visual system can certainly result safer and more reliable than any existing digital device.

References